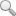陜西土木建筑網首頁 > 學術研究 > 課題研究 > 廣州新電視塔細腰段橫向水平支撐有效性研究

摘要：廣州新電視塔采用的是鋼結構外框筒和鋼筋混凝土核心筒組成的筒中筒結構體系，整個結構外框筒細長、細腰及扭腰。在中部細腰段區域(約160 m高度)，原結構方案在內外筒之間不設置任何橫向水平支撐，這將導致細腰段區域的穩定承載力非常低下。...

廣州新電視塔細腰段橫向水平支撐有效性研究

劉祿宇  郭彥林  王永海   林冰

 清華大學　北京100084

引言

    廣州新電視塔采用的是鋼結構外框筒和鋼筋混凝土核心筒組成的筒中筒結構體系，其突出特點是整個塔身細長、細腰及扭腰，呈兩端大中間小的形狀，其中“細腰”段部分透空區高達166.4m。在結構初步設計中，其細腰段完全透空，在相應高度范圍內外框筒和核心筒之問沒有任何橫向支撐連接，兩者處于相互獨立的狀態。對于外框筒立柱而言，其在環向(面內)由與之相鄰的環梁和斜撐提供較強的約束，而在面外僅靠環梁的環箍作用提供支撐，因而易發生沿著面外的失穩。細腰段外框筒鋼結構的穩定問題一度成為結構設計人員關注的焦點。在后續的深化設計中，細腰段透空區的內外筒之間增設了4道橫向水平支撐構件，為立柱提供了面外的支撐作用，提高了細腰段外框筒鋼結構的穩定性。但增設4道橫向水平支撐構件后，細腰段的穩定承載力能否保證整體結構設計既安全又經濟便成為本文研究的重點。

    本文應用有限元方法進行了風荷載工況下塔體結構的整體彈性屈曲分析，然后，將細腰段作為一個結構單元，進行細腰段透空區的彈性屈曲分析及二階彈塑性極限承載力分析，研究了不同道數的支撐布置對細腰段外框筒結構彈性穩定性能和彈塑性穩定性能的影響，全面評價支撐設置的有效性與合理性，為電視塔細腰段外框筒結構設計提供了理論依據。

1、支撐布置及有限元模型

　　在整個塔體結構中，細腰段結構總高度為l66.4m，其底部和頂部為組合樓面，標高分別為168.0m、334.4m。4道橫向撐桿沿該區域高度方向均勻布置，支撐布置不在一個平面內，以與核心筒上的旋轉樓梯的布置相協調。支撐中心標高分別為202.5m、234.3m、266.8m、305.6m，將細腰段劃分為3-1～3—5共5個區域，見圖l(a)。撐桿分別與外框筒立柱、核心筒鋼骨連接，連接形式采用鉸接節點，見圖l(b)。撐桿采用圓管(截面l一咖402×16)、箱形(截面2—950×400×25×25和截面3—560×350×20×20)、工形(截面4—380×300×12×20)3種截面形式，共4種截面尺寸。截面1和截面2為主要桿件，其中截面l撐桿布置在內外筒距離較小的區域，撐桿長度較小；而截面2撐桿布置在內外筒距離較大的區域，撐桿長度較大。為了減小撐桿的計算長度，在撐桿之間設置了輔撐(截面4)，以提高撐桿的穩定性。

    支撐將起到聯系內外筒的作用，通過支撐的受壓或受拉協調兩者的變形，為外框筒立柱提供面外約束，以減小立柱的計算長度，提高其穩定性。支撐兩端鉸接，在進行彈塑性穩定承載力分析時，參考《鋼結構設計規范》(GB 50017--2003)，對支撐施加缺陷幅值為構件長度1/l000的幾何初始缺陷。

　　本文將改變支撐布置的道數，研究不同支撐道數對細腰段穩定性能的影響，進而考察設置4道水平支撐的合理性。

    首先進行風荷載工況下塔體的整體彈性屈曲分析，根據細腰段的屈曲變形確定增設l道支撐的高度位置，其設置l道支撐的最有效位置將根據無支撐布置時細腰段的屈曲波形確定。

    塔體的整體有限元模型見圖2(a)，荷載工況取為1.2恒荷載+1.4風荷載+0.98活荷載(風荷載工況，結構設計中的最不利荷載工況)。其中恒荷載考慮了結構構件的自重以及樓板面層等附加恒荷載；活荷載為使用荷載。風荷載方向為X軸負方向，是風荷載最不利的作用方向。在進行塔體結構的整體彈性屈曲分析時，豎向荷載和水平風荷載將同比例增加。

    然后，將細腰段作為一個結構單元進行彈性屈曲分析及彈塑性極限承載力分析。細腰段有限元模型見圖2(b)，其邊界條件和荷載的確定過程見后續文章，本文不再贅述。立柱柱頂與頂部加載盤鉸接連接，柱腳和基座鉸接；核心筒底部采用轉動彈簧連接，計算分析中采用彈性彈簧單元模擬(見圖3)。

    考慮到外框筒是主要研究對象，而核心筒僅提供抗側和抗扭剛度，因此核心筒頂部節點和加載盤相應位置節點耦合水平面內的x、y方向平動自由度，釋放其他自由度，以保證水平力由兩者共同承擔，同時為外框筒結構提供抗扭剛度貢獻，而軸力和彎矩僅傳遞給外框筒結構。細腰段承受的荷載包括豎向荷載產生的外框筒軸力N、水平風荷載產生的外框筒彎矩M和內外筒合剪力V，荷載組合取為軸力N、彎矩M和剪力V同比例施加。根據研究，x軸負方向的承載力可作為評價結構弱軸方向承載能力的依據，因而在本文的分析中，將水平荷載方向取為x軸負方向，保持與塔體的整體彈性屈曲分析工況一致，以便進行整體屈曲分析與細腰段屈曲分析結果的比較。

 

　　在進行細腰段彈塑性穩定承載力分析時，需引入幾何初始缺陷。對于細腰段而言，其穩定極限承載力對幾何初始缺陷很不敏感，這是因為結構體形不規則，且構件傾斜布置，其形心軸為空間曲線，相當于結構本身即存在較大的初始缺陷。因此，本文在進行彈塑性穩定承載力分析時將不再對細腰段結構單元施加整體的幾何初始缺陷，而僅給支撐施加初始缺陷。

2、整體結構屈曲分析

    首先進行無支撐布置時塔體的整體彈性屈曲分析，然后通過分析細腰段外框筒結構發生屈曲時的屈曲模態，根據其屈曲波形確定分別設置1～4道支撐時最有效的支撐高度位置。

　　2.1無支撐

    圖4給出了無支撐布置時結構的屈曲模態。結構整體細長，因而第一階屈曲模態為繞弱軸的整體彎曲屈曲變形；第二、三階為細腰段外框筒鋼結構的局部屈曲，屈曲變形為透空區3-1～3—3外框筒的多波形凹進凸出變形，且主要變形集中在透空區3-1—3-2，而3—3變形相對較小；第四階為底部透空區鋼外框筒的片狀局部屈曲。

 

　　可見，無支撐布置時，在所有透空區中，細腰段和底部透空區外框筒結構的受力最為不利，穩定問題最為突出。細腰段受力較大，且在所有透空區中高度最大，因而容易發生屈曲，而在細腰段中3—1～3-3區域最容易發生屈曲，一方面因為該區域位于細腰段底部，風荷載傾覆力矩產生的立柱軸壓力較大；另一方面，在整個細腰段中其平面輪廓尺寸最大，環梁、斜撐對立柱約束作用較弱。底部透空區屈曲變形為兩個剛性樓層之問外框筒的局部屈曲，在整個結構中該透空區承受的荷載最大，在高度達57.2 m的透空區范圍內，外框筒無徑向約束，是除細腰段透空區外高度最大的區域，故外框筒較易發生屈曲。無支撐布置時底部透空區對應的屈曲荷載僅比細腰段高7％，在細腰段設置支撐的情況下，兩個透空區中哪個最先發生屈曲取決于支撐布置對細腰段外框筒結構穩定性的提高程度。

    根據無支撐布置時細腰段屈曲變形的特點：屈曲變形為透空區3-1～3—3外框筒的多波形凹進凸出變形，且主要變形集中在透空區3-1～3-2，而3—3變形相對較小，確定分別設置l～3道支撐時最有效的布置形式，如圖5所示。1道時布置在HC2位置，2道時布置在HCl、HC2位置，3道時布置在HCl～HC3位置。

 

圖5不同道數的支撐布置形式

　　2.21～4道支撐

    表1和圖6給出了風荷載作用下不同道數支撐布置時整體結構的屈曲分析結果，屈曲荷載采用屈曲荷載值與荷載設計值的比值Pcr/Po來表示。

    支撐布置主要影響細腰段的彈性穩定性能，包括對應的屈曲荷載和屈曲模態，支撐道數不大于3時，隨著支撐道數的增加，細腰段屈曲模態對應的屈曲荷載值越來越大，且高于底部透空區對應的屈曲荷載，可見支撐的布置提高了細腰段的穩定性能，改變了兩區域的彈性屈曲先后順序(見表l)。支撐道數大于3時，新增設的支撐對細腰段屈鹽荷載幾乎沒有影響(見圖6)。此外，支撐布置的道數對結構的整體彎曲屈曲和底部透空區的局部屈曲影響甚微，不同支撐布置時屈曲荷載和屈曲模態基本相同。下文中將僅列出細腰段發生屈曲的模態。

表1整體彈性屈曲分析結果統計表

 

圖6  支撐布置道數對細腰段屈曲荷載的影響

    綜合不同道數支撐的分析結果，可得到以下主要結論：

    (1)相比無支撐布置，只設置1道支撐(HC2)時的屈曲荷載值提高了11.5％，且屈曲荷載值高于底部透空區屈曲模態對應的荷載值，表明加設的1道支撐改變了兩區域的彈性屈曲先后順序。屈曲變形為透空區3-1～3-2和3-3～3_4的兩段波形(見圖7a)，在支撐HC2的高度由于支撐的存在變形幾乎為零，導致波形不連續。

    (2)相比l道支撐布置，設置2道支撐(HCl、 HC2)時的屈曲荷載值提高了3．6％，屈曲變形為集中在透空區3-3～3—5的單個半波形(見圖7b)，表明底部兩道支撐的設置有效地提高了透空區3-1～3-2的彈性穩定性。

    (3)相比2道支撐布置，設置3道支撐(HCl～HC3)時的屈曲荷載值提高了7．6％，屈曲變形為集中在透空區3—1～3-3的3個半波(圖7c)，完整的屈曲半波發生在樓層和支撐層之間，而沒有表現出透空區3—1～3-3大片桿件的凹進或凸出，說明增設的3道支撐為外框筒提供了有效的面外支撐作用。

    (4)4道支撐時(實際設計)的細腰段第一階屈曲模態對應的屈曲荷載值和3道的相同，且屈曲變形(見圖7d)類似，高階的荷載值差別也很小，說明增設的支撐對提高細腰段外框筒結構的彈性穩定性能不明顯，3道支撐設置最有效。

3、細腰段屈曲分析

　　本節將細腰段作為一個結構單元，研究其在不同道數支撐布置下的彈性穩定性能。圖8將不同道數支撐布置時細腰段屈曲分析和整體屈曲分析結果進行比較，可見兩者的屈曲荷載值很接近，差值在5％以內，說明從整體結構中提取細腰段作為一個結構單元進行分析的方法可以準確、合理地評估其承載能力。無支撐布置時前者的屈曲荷載值偏低，1～4道支撐布置時前者的屈曲荷載值偏高，支撐道數對細腰段屈曲荷載的影響規律與整體屈曲分析結果類似。設置4道支撐時細腰段的屈曲荷載值和3道的相同，說明設置3道支撐對于提高細腰段外框筒結構的彈性穩定性最有效，與整體屈曲分析的結論是一致。

 

圖8細腰段屈曲分析與整體屈曲分析荷載值的比較

    此外，通過比較不同道數支撐布置時整體屈曲分析和細腰段屈曲分析得到的細腰段屈曲模態(見圖9)，可以發現兩者屈曲變形的位置和形式是類似的。    以上分析僅為彈性屈曲分析結果，是否說明在細腰段透空區設置3道支撐就是最經濟的呢?這不盡然，還需要通過彈塑性穩定承載力分析進一步確定。

4、細腰段穩定承載力研究

    以細腰段筒體為基本單元，進行不同道數支撐布置時細腰段的穩定承載力研究，分析工況取為具有代表性的荷載工況(荷載沿著x軸負方向)：軸力N、彎矩M和剪力V同比例施加直至結構破壞。

    穩定極限承載力與荷載設計值的比值Pu／Po可作為評價結構安全儲備的標準。穩定承載力隨著所設置支撐道數的增加而增大(見圖l0)，僅增設l道支撐對承載力的提高幅度分別為8.8％、3.6％、8.6％和9.6％。圖1 1給出了不同支撐布置時細腰段頂部加載盤中心點的荷載一位移曲線。

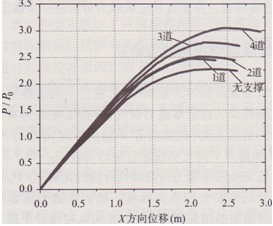
圖11  不同支撐布置時的荷載一位移曲線     

    不同支撐布置時失穩時刻細腰段的結構變形和應力分布。無支撐布置時，結構的變形以彎曲變形為主，同時外框筒頂部發生了明顯的順時針方向扭轉變形，該區域大部分構件已受壓或受拉進入屈服；結構底部受壓一側部分立柱鋼管和斜撐也已受壓進入屈服，由于取定的荷載工況下荷載的偏心距較小，因而受拉一側構件仍處在彈性受力狀態。

5、結論

    本文應用有限元方法進行風荷載工況下塔體的整體彈性屈曲分析、細腰段透空區的彈性屈曲分析及二階彈塑性極限承載力分析，研究了不同道數的支撐布置對細腰段外框筒結構彈性穩定和彈塑性穩定性能的影響，可得到以下主要結論：

　　(1)通過不同支撐布置時塔體的整體彈性屈曲分析，獲得了細腰段屈曲模態對應的屈曲荷載，分析了支撐道數對細腰段屈曲荷載的影響規律。根據無支撐布置時細腰段外框筒結構的屈曲變形，確定了分別設置l～4道支撐時最有效的支撐高度位置。與無支撐相比，4道支撐布置時的屈曲荷載值提高了24.3％。

　　(2)將細腰段作為一個結構單元，通過不同支撐布置時細腰段透空區的彈性屈曲分析，獲得了支撐道數對屈曲荷載的影響規律。與無支撐相比，4道支撐布置時的屈曲荷載值提高了27.3％。

    (3)將塔體的整體彈性屈曲分析和細腰段透空區彈性屈曲分析結果進行比較，兩者的屈曲荷載值很接近，差值在5％以內，說明從整體結構中提取細腰段作為一個結構單元進行分析的方法可以準確、合理地評估其承載能力。

參考文獻

[1]劉祿宇．廣州新電視塔細腰段穩定承載力試驗及理論研究[D]．北京：清華大學，2007

[2] ARUP工程顧問有限公司，廣州市設計院．廣州新電視塔初步設計[R]．2005(ARUP，Guangzhou DesignInstitute．Initial design of Guangzhou New TV Tower[R]．2005(in Chinese))

[3]GB 50017--2003鋼結構設計規范[S]．北京：中國計劃出版社，2003

[4]陳紹蕃．鋼結構穩定設計指南[M]．北京：中國建筑工業出版社，2004

(本文來源：陜西省土木建筑學會  文徑網絡：溫紅娟  劉紅娟  尹維維 編輯 文徑 審核)

上一篇： 不同溫濕度環境粉煤灰混凝土與基準混凝土收縮性能試驗研究

下一篇： 從汶川地震提高建筑結構抗倒塌能力的必要性和可行性